Recently, I was asked to determine the extent to which seasonality influenced a particular time series. No problem, right? The statsmodels Python package has a seasonal_decompose function that seemed pretty handy; and there’s always Google! As it turns out, this was a bit trickier than I expected. In this post I’ll share some of the problems I encountered while working on this project and how I solved them.
In attempting to find posts or papers that addressed quantifying the extent to which the time series was driven by seasonality, every example I came across fell into one of two categories:
- Here’s a few lines of code that produce a visualization of a time series decomposition.
- Here’s how you can remove the seasonality component of a time series, thus stabilizing your time series before building a predictive model.
Also, each example started with “Here’s a time series with a seasonal trend.” Not super helpful for when you’re trying to determine how much seasonality drives a particular time series.
What I couldn’t find was anything that definitively stated how to quantify the extent to which a time series was driven by seasonality. I found some conflicting information about seasonal indexing, and decided to move on. Granted, if I had continued looking, I imagine that eventually I would have found something. But instead, I decided to experiment!
Series Decomposition
To start out, I decomposed the time series into its trend, seasonality, and noise components. Here’s an example of what that looks like.

How seasonal is this time series? ¯\_(ツ)_/¯
At first glance, it looks like the data is obviously seasonal, judging by the periodicity in the seasonal decomposition component. But, in Googling several examples of seasonal decomposition, every seasonal component I came across displayed periodicity.
So, I made a time series of random data points between 0 and 1000, and decomposed that. Here’s what that looks like.

Holy periodicity, Batman!
It also displays periodicity! But, if we look at the y axis in each of these components, note that the noise component has the largest range in the random time series.
However, in the time series in question, the seasonal component has a much smaller range than the trend or the noise.
- Trend range = 2000 (3000 to 5000)
- Seasonal range = 500 (-250 to 250)
- Noise range = 2000 (-1000 to 1000)
(I noticed that the trend and noise ranges have the same magnitude here, but I don’t know what that means. If you know, I’d love to hear about it in the comments!)
Just for fun, here’s the decomposition for a time series that is completely seasonal. Every January has a value of 100, increasing by 100 each month until reaching 1200 in December, and falling back to 100 again January.

Purely seasonal time series. Makes sense.
The trend and noise components are a constant value of 0, as you would expect in data that is driven purely by a seasonal trend.
Given that our series looks much closer to the random data than it does to the purely seasonal data, the results of the seasonal decomposition seem to point to a weak seasonality, if any. At this point in the analysis, I’m a little skeptical of the conclusions here, so, I decided to look for more evidence. On to another method!
De-trending
This is the process of removing the trend dependency that may be present within a time series. I used the differencing method to inspect the trend dependencies of our data.
Imagine you have a data set with a strong yearly seasonal trend. If you want to predict what the value for June will be, looking at the value from June last year will give you the most information about what you can expect.
Now imagine you have a trend that doesn’t fluctuate in a periodic way, it simply increases or decreases. If you wanted to predict your sales for June, you would get more information from looking at the month(s) directly preceding June, than from looking at June from last year.
Both of these trends can be removed from a time series. In differencing, you are basically subtracting the most relevant previous values to account for the trend.
For example, removing an “up-and-to-the-right” trend from a time series essentially rotates the graph until it’s flat, leaving the “right,” but stabilizing the “up.” Removing a seasonal trend basically smooths out the bumps in the graph. De-trending a time series is often used to produce a stationary series from which you can build a forecasting model. Here’s an example of removing an up-and-to-the-right trend from a data set.
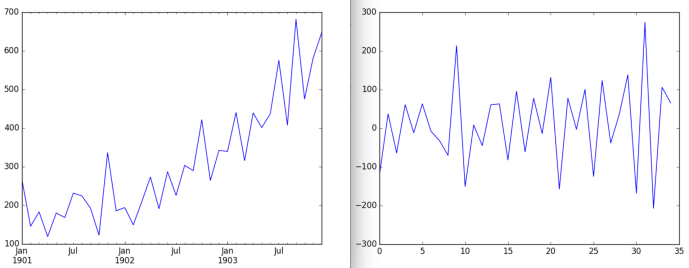
Before and after: stabilizing a time series
So, I reasoned, by removing a particular type of trend and comparing the resulting series with the original, we could make a judgement about the amount of “influence” the particular series has on the original time series.
Here’s how each differencing process affects the series. I’ve included a plot of the original series for reference.

Comparison of de-trending results
From these figures it looks like removing the daily trend (or just trend component as we’ve been referring to it) has more affect on the original series than removing a seasonal trend. There is some affect from removing a seasonal trend, though. So, this reinforced my earlier conclusion; that if there is seasonality in this data, it’s weak compared to the overall trend.
To me, this didn’t seem completely thorough, so I checked one more thing.
Autocorrelation function
Over that weekend, while having monthly math beers (Yes! That’s a thing!), one of my grad school friends recommended that I look at the autocorrelation function, or ACF.
The autocorrelation function shows how well a data set correlates to a time-shifted version of itself. It calculates this correlation for many possible time shifts, known as lags, and surfaces repeating patterns of correlation.
Returning to our manufactured data sets, the ACF for our purely seasonal time series looks like this.

ACF of a very seasonal time series
Notice the spikes at intervals of 12. This means that the correlation between the original series and its shifted version is highest when that shift is a multiple of 12 time periods (in our case months), indicating a yearly seasonal trend.
The blue region in these graphs represents the confidence intervals around these correlation measures. Spikes that fall outside of this cone, are less likely to be due to chance.
Keeping that in mind, let’s look at the ACF for the random series.

ACF of a randomly generated time series
Here, there are some spikes but they are all very firmly within the cone, so this ACF does not support the presence of a seasonal trend.
Here’s the ACF of our time series.

ACF of our time series
We see a few spike like areas, but, most are all within the cone. The spikes outside of the cone are for versions shifted by much smaller intervals than 12, meaning that as you shift the data farther from itself the correlation decreases. This suggests to me that the general trend of the time series has a much stronger influence on the series than a seasonal trend.
So, in short, (just kidding, very long!) I didn’t find overwhelming evidence that seasonality plays much of a role in our series. But even though I didn’t find anything, (because let’s face it, that’s more often the case than not), I found it to be a really interesting analysis. Does that ever happen to you?
Reblogged this on Boris Gorelik and commented:
Excellent piece (part one of three) about time series analysis by my colleague Carly Stambaugh
LikeLike